1. Point Symmetry: Two distinct points, P and P1, are symmetric about point M if and only if M is the midpoint of P and P1 (rotational 180 degree symmetry).
2. Line Symmetry: Two distinct points, P and P1, are symmetric about a line if and only if the line is perpendicular to the bisector of P and P1
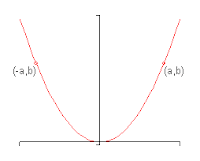
3. Origin Symmetry Test: make both the x and y variable negative then solve for y
4. X Asix Symmetry Test: make the y variable negative then solve for y
5. Y Axis Symmetry Test:make the x variable negative then solve for y
6. Y=X Symmetry Test: exchange the x and then solve for y
7. Y=-X Symmetry test: exchange the x and y and make them opposite then solve for y
8. Odd Function: a function is odd if and only if f(-x)=-f(x)
9. Even Function: a function is even if and only if f(-x)= f(x)
10. Inverse Relations: two relations and inverse relations if and only if one relation contains the element (b, a) whenever the other relation contains the element (a, b)
11. Rational Function: a function is rational if and only if it is the quotient of two polynomials
12. Asymptote: a line a graph approaches but never reaches
13. Horizontal Asymptote: if f(x)=b then there is a horizontal asymptote at y=b x=infinity
14. Vertical Asymptote: if limit f(x)= infinity, then there is a veritcal asymptote at x=a
15. Increasing Function: a function where f(x1) is less than f(x2) when x1 is less than x2
16. Decreasing Function: a function where f(x1) is greater than f(x2) when x1 is less than x2
17. Maximum: a point on a curve where a function changes from increasing to decreasing
18. Minimum: a point on a curve where function changes from decreasing to increasing
19. Absolute Maximum/Minimum: highest/lowest point on a curve; also called Global Max/Min
20. Relative Maximum/Minimum: highest/lowest point within a specific interval; also called Local Max/Min
21. Concave Up: a graph is concave up if and only if the slope is increasing
22. Concave Down: a graph is concave down if and only if the slope is decreasing
23. Point of Inflection: a point on a graph where the concavity changes
24. Continuous: a graph is continuous is there are no point or jump discontinuities
25. End Behavior: how y acts as x approaches a value
26. Angle Measure: measure of the rotation of the terminal side of an angle from the initial side of an angle; typically measured in degrees or radians
27. Standard Position: an angle with its vertex on the origin and its initial side on the positive x axis
28. Quadrantal Angle: an angle whose terminal side is on an axis
29. Radian: angle measure that produces an arc the length of the radius; the angle measure is the same no matter the size of the circle
30. Coterminal Angles: angles that have the same terminal ray in standard position
31. Reference Angle: the acute angle formed by the terminal side of an angle and the x axis
32. Arc Length Formulas: y=C(x/360) where x is the central angle in degrees
y= C(xr/2pi) where x is the central angle in radians
33. Sector Area Formulas: y= pi(r)(r)(x/360) where x is the central angle in degrees
y= pi(r)(r)(x/2pi) where x is the central angle in radians
34. Linear Velocity: the rate an object moves on a straight path
35. Linear Velocity Formula: r= d/t
36. Angular Velocity: the change in an angle over time; revolutions/time
37.1: Sine: opposite leg over hypotenuse; y/r
37.2: Cosine: adjacent leg over hypotenuse; x/r
37.3: Tangent: opposite leg over adjacent leg: y/r
37.4: Cosecant: hypotenuse over opposite; reciprocal of sine; r/y
37.5: Secant: hypotenuse over adjacent; reciproal of cosine; r/x
37.6: Cotangent: adjacent over opposite; reciprocal of tangent; x/y
38. Unit Circle: circle with a radius of 1 and center origin
39. Law of Sines: sinA/a = sinB/b = sinC/c
40. Law of Cosines: c squared = a sqaured + b squared - 2abcosC
41. Heading/Bearing: the angle of direction clockwise from north
42. Area of a Triangle: using SAS, .5absinC
43. Area of a Segment of a Circle: A= .5 (x-sinx) (r)(r)
44. Amplitude: the vertical stretch of a graph
45. y=Arcsinx: -pi/2 is less than or equal to y is less than or equal to pi/2; quad I and IV
46. y=Arccosx: 0 is less than or equal to y is less than or equal to pi; quad I and II
47. y=Arctanx: -pi/2 is less than or equal to y is less than or equal to pi/2; quad I and IV
NOTE: Finding images for the identities was pretty much impossible and pointless so there are none
48. Reciprocal IDs: secx= 1/cosx cscx= 1/sinx cotx= 1/tanx
49. Quotient IDs: tanx= sinx/cosx cotx= cosx/sinx
50. Pythagorean IDs: (sin)(sin)x + (cos)(cos)x= 1
1 + cot(cot)x= (csc)(csc)x
(tan)(tan)x + 1= (sec)(sec)x
51. Opposite IDs: sin(-x)= -sinx ODD cos(-x)=cos(x) EVEN
52. Translation IDs: sin(x+90)= cosx cos(x-90)=sinx
53. Cosine Difference ID: cos(x-B)= cosxcosB+sinxsinB
54. Cosine Sum ID: cos(x+B)= cosxcosB-sinxsinB
55. Sine Sum ID: sin(x+B)= cosxsinB+cosBsinx
56. Sine Differene ID: sin(x-B)= cosxsinB-cosBsinx
57. Sine Double Angle Formula: sin2x= 2sinxcosx
58. Cosine Double Angle Formula: cos2x= (cos)(cos)x - (sin)(sin)x
1- 2(sin)(sin)x
-1 + 2(cos)(cos)x
59. Vector: quantity that has magnitude and direction
60. Equal Vectors: two vectors with the same amplitude (angle) and magnitude
61. Opposite Vectors: two vectors with the same magnitude and opposite directions
62. Horizonal Component: abs(V)= cosx
63. Vertical Componen: abs(V)= sinx
64. Equilibrium: forces are at equilibrium if and only if their sum is 0
65. Parametric Equation: x and y are functions of a third variable, t
66. Projectile Formula: x= t(vcosx) + x
y= -.5g(t)(t) + t(vsinx) + y
67. Properties of Exponents
Product Property: (a^m)(a^n)=a^(m+n)
Power of a power property: (a^m)^n= a^(mn)
Power of a quotient property: (a/b)^m= (a^m)/(b^m) b is not equal to 0
Power of a product property: (ab)^m= (a^m)(b^m)
Quotient Property: (a^m)/(a^n)= a^(m-n) b is not equal to 0
68. Definition of b^(1/n): For any real number where b is greater than or equal to 0 and any integer where n is greater than 1, b^(1/n)= n route of b
69. Definition of Rational Exponents: For any real number b and any integers m and n with n greater than 1, b^(m/n)=n route of b^m=(n route of b)^m
70. Present Value Formula: Pn= P(((1-(1+i)^-n)/i)
Pn= sum of present value
P= payment
i= interest rate per period
n= total number of payments
71. Future Value Formula: Fn= P((((1+i)^n)-1)/i)
Fn= sum of future value
P= payment
i= interest rate per period
n= total number of payments
72. e=lim(1+ 1/n)^n where n can be infinite
73. Properties of Logs:
Product Property: log base b of m + log base b of n = log base b of mn
Quotient Property: log base b of m/n = log base b of m - log base b of n